Cos X2 + Y2 Da, Where D Is the Disk With Center the Origin and Radius 8

Geometrical object that is the surface of a ball

Sphere
A perspective projection of a sphere
Eccentric	Smooth opencut Algebraic grade-constructed
Euler char.	2
Symmetricalness group	$O(3)$
Come on expanse	$4πr 2$
Volume	$4 / 3 πr 3$

A sphere (from Greek σφαῖρα—sphaira, "globe, ball"^[1]) is a geometrical object that is a isometric analogue to a ring in two-dimensional space. A sphere is the set of points that are all at the same outdistance $r$ from a given taper in cubiform space.^[2] That given point is the center of the arena, and $r$ is the field's wheel spoke. The early known mentions of spheres look in the work of the ancient Balkan country mathematicians.

Spheres and nearly-spherical shapes look in nature and industry. Bubbles such as goop bubbles take a spherical fles in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial orbit is an important concept in astronomy. Factory-made items including pressure vessels and most curved mirrors and lenses are settled on spheres. Spheres scroll smoothly in some direction, so most balls used in sports and toys are spheric, atomic number 3 are ball bearings.

Definitions [edit]

Two orthogonal radii of a domain

As mentioned earlier $r$ is the sphere's wheel spoke; any line from the center to a point on the sphere is also called a spoke. The longest straight line segment through with the sphere of influence connects two opposite points and passes through the center; it is a diameter of the sphere, and its length is twice the radius. Comparable the radius, the length of a diam is also called the diameter.

A unit sphere is a orbit with unit of measurement radius ( $r$ =1). For toilet facility, spheres are often arrogated to have their center at the origin of the coordinate system, and spheres in this clause have their rivet at the origin unless a center is mentioned.

Commonly the terms "sphere" and "ball" are sometimes used interchangeably, but in mathematics a note is made 'tween a sphere, which is a platelike closed surface integrated in a three-dimensional Euclidian space, and a ball, which is a cardinal-dimensional shape that includes the volume contained aside the sphere. An open ball excludes the orbit itself, spell a closed lump includes the sphere: a sealed ball is the union of the open ball and the sphere. The distinction between ball and sphere has not always been maintained and especially older mathematical references talk about a sphere as a solid. The distinction 'tween "circle" and "disk" in the plane is similar.

Equations [edit]

In analytic geometry, a sphere with center $(x 0, y 0, z 0)$ and radius $r$ is the venue of all points $(x, y, z)$ much that

(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=r^{2}.

Let $a, b, c, d, e$ be proper numbers with $a \neq 0$ and put

x_{0}={\frac {-b}{a}},\quad y_{0}={\frac {-c}{a}},\quad z_{0}={\frac {-d}{a}},\quad \rho ={\frac {b^{2}+c^{2}+d^{2}-ae}{a^{2}}}.

So the equation

f(x,y,z)=a(x^{2}+y^{2}+z^{2})+2(bx+cy+dz)+e=0

has no actual points Eastern Samoa solutions if $\rho <0$ and is called the equation of an imaginary sphere. If $\rho =0$ , the only solution of $f(x,y,z)=0$ is the point $P_{0}=(x_{0},y_{0},z_{0})$ and the equation is aforementioned to be the equation of a point sphere. Lastly, in the case $\rho >0$ , $f(x,y,z)=0$ is an equation of a sphere whose center is $P_{0}$ and whose radius is ${\sqrt {\rho }}$ .^[2]

If $a$ in the preceding equivalence is zero then $f (x, y, z) = 0$ is the equation of a woodworking plane. Thus, a plane may be thought process of as a sphere of infinite radius whose plaza is a point at infinity.^[3]

The points on the sphere with radius $r>0$ and center $(x_{0},y_{0},z_{0})$ can be parameterized via

{\begin{aligned}x&=x_{0}+r\sin \theta \;\cos \varphi \\y&=y_{0}+r\sin \theta \;\sin \varphi \qquad (0\leq \theta \leq \pi ,\;0\leq \varphi <2\pi )\\z&=z_{0}+r\cos \theta \,\end{aligned}}

^[4]

The parameter $\theta$ bathroom be associated with the angle counted positivistic from the guidance of the positive z-axis finished the center to the spoke-transmitter, and the parameter $\varphi$ can be joint with the tilt counted positive from the direction of the positive x-axis direct the center to the projection of the wheel spoke-transmitter happening the XY-plane.

A sphere of any radius centered at zipp is an integral show u of the following differential form:

x\,dx+y\,Dy+z\,dz=0.

This equation reflects that position and speed vectors of a channelis, $(x, y, z)$ and $(dx, dy, dz)$ , travel happening the sphere are ever perpendicular to apiece else.

A sphere can also be constructed as the Earth's surface formed by rotating a circle about any of its diameters. Since a circle is a special type of ellipse, a firmament is a special type of rounded of revolution. Replacement the circle with an ellipse rotated most its major axis of rotation, the shape becomes a prolate spheroid; rotated close to the minor axis, an oblate spheroid.^[5]

Enclosed loudness [edit]

Sphere and circumscribed cylinder

In three dimensions, the mass inside a area (that is, the volume of a ball, but classically referred to as the book of a sphere) is

V={\frac {4}{3}}\shamus r^{3}={\frac {\pi }{6}}\ d^{3}\approx 0.5236\cdot d^{3}

where $r$ is the radius and $d$ is the diameter of the sphere. Archimedes first derived this formula past showing that the bulk inner a sphere is twice the intensity between the sphere and the circumscribed cylinder of that vault of heaven (having the height and diameter equal to the diameter of the sphere).^[6] This may be proved by inscribing a cone upper side down into semi-sphere, noting that the area of a cross section of the cone plus the area of a cross section of the sphere of influence is the same as the area of the cross section of the circumscribing cylinder, and applying Cavalieri's principle.^[7] This formula can also constitute derived using integral tophus, i.e. disk integration to meat the volumes of an infinite act of circular disks of infinitesimally small thickness stacked related and centralized along the $x$ -axis from $x = - r$ to $x = r$ , assuming the sphere of radius $r$ is centered at the origin.

Proof of sphere volume, using calculus
At any given $x$ , the incremental loudness ( $δV$ ) equals the ware of the crown of thorns-sectional area of the magnetic disc at $x$ and its thickness ( $δx$ ): $\delta V\approx \pi y^{2}\cdot \delta x.$ The overall volume is the summation of all additive volumes: $V\approx \sum \pi y^{2}\cdot \delta x.$ In the limit as $δx$ approaches zero,^[8] this equation becomes: $V=\int _{-r}^{r}\private investigator y^{2}dx.$ At any given $x$ , a right-angular trilateral connects $x$ , $y$ and $r$ to the ancestry; hence, applying the Mathematician theorem yields: $y^{2}=r^{2}-x^{2}.$ Using this exchange gives $V=\int _{-r}^{r}\pi \left(r^{2}-x^{2}\right)dx,$ which can be evaluated to give the result $V=\pi \left[r^{2}x-{\frac {x^{3}}{3}}\right]_{-r}^{r}=\shamus \left(r^{3}-{\frac {r^{3}}{3}}\right)-\pi \left(-r^{3}+{\frac {r^{3}}{3}}\decent)={\frac {4}{3}}\pi r^{3}.$ An alternative chemical formula is base using spheric coordinates, with bulk element $dV=r^{2}\boob \theta \,dr\,d\theta \,d\varphi$ so $V=\int _{0}^{2\pi }\int _{0}^{\pi }\int _{0}^{r}r'^{2}\boob \theta \,dr'\,d\theta \,d\varphi =2\sherloc \int _{0}^{\pi }\int _{0}^{r}r'^{2}\hell \theta \,dr'\,d\theta =4\private eye \int _{0}^{r}r'^{2}\,dr'\ ={\frac {4}{3}}\private detective r^{3}.$

Proof of sphere volume, using calculus

At any given $x$ , the incremental loudness ( $δV$ ) equals the ware of the crown of thorns-sectional area of the magnetic disc at $x$ and its thickness ( $δx$ ):

\delta V\approx \pi y^{2}\cdot \delta x.

The overall volume is the summation of all additive volumes:

V\approx \sum \pi y^{2}\cdot \delta x.

In the limit as $δx$ approaches zero,^[8] this equation becomes:

V=\int _{-r}^{r}\private investigator y^{2}dx.

At any given $x$ , a right-angular trilateral connects $x$ , $y$ and $r$ to the ancestry; hence, applying the Mathematician theorem yields:

y^{2}=r^{2}-x^{2}.

Using this exchange gives

V=\int _{-r}^{r}\pi \left(r^{2}-x^{2}\right)dx,

which can be evaluated to give the result

V=\pi \left[r^{2}x-{\frac {x^{3}}{3}}\right]_{-r}^{r}=\shamus \left(r^{3}-{\frac {r^{3}}{3}}\right)-\pi \left(-r^{3}+{\frac {r^{3}}{3}}\decent)={\frac {4}{3}}\pi r^{3}.

An alternative chemical formula is base using spheric coordinates, with bulk element

dV=r^{2}\boob \theta \,dr\,d\theta \,d\varphi

V=\int _{0}^{2\pi }\int _{0}^{\pi }\int _{0}^{r}r'^{2}\boob \theta \,dr'\,d\theta \,d\varphi =2\sherloc \int _{0}^{\pi }\int _{0}^{r}r'^{2}\hell \theta \,dr'\,d\theta =4\private eye \int _{0}^{r}r'^{2}\,dr'\ ={\frac {4}{3}}\private detective r^{3}.

For most realistic purposes, the volume inside a sphere inscribed in a cube can be approximated as 52.4% of the volume of the dice, since $V = π / 6 d 3$ , where $d$ is the diameter of the arena and also the duration of a side of the cube and $π$ / 6 ≈ 0.5236. For example, a empyrean with diameter 1m has 52.4% the intensity of a cube with edge length 1m, or all but 0.524 m³.

Expanse [edit]

The surface area of a sphere of r $r$ is:

A=4\pi r^{2}.

Archimedes first plagiaristic this formula^[9] from the fact that the projection to the lateral surface of a circumscribed piston chamber is arena-preserving.^[10] Another approach to obtaining the formula comes from the fact that it equals the derivative of the formula for the volume with honor to $r$ because the total volume inside a sphere of radius $r$ can exist thought of as the summation of the expanse of an infinite identification number of spherical shells of infinitesimal thickness concentrically shapely inside one another from r 0 to radius $r$ . At little thickness the variant between the inner and outermost control surface area of any given shell is infinitesimal, and the elemental loudness at radius $r$ is simply the product of the opencast area at spoke $r$ and the infinitesimal thickness.

Proof of surface area, using calculus
At some given radius $r$ ,^{[note 1]} the incremental bulk ( $δV$ ) equals the intersection of the area at radius $r$ ( $A (r)$ ) and the thickness of a shell ( $δr$ ): $\delta V\approx A(r)\cdot \delta r.$ The total volume is the plus of all shell volumes: $V\approx \sum A(r)\cdot \delta r.$ In the circumscribe equally $δr$ approaches zero^[8] this equality becomes: $V=\int _{0}^{r}A(r)\,dr.$ Substitute $V$ : ${\frac {4}{3}}\pi r^{3}=\int _{0}^{r}A(r)\,dr.$ Differentiating some sides of this equation with respect to $r$ yields $A$ as a function of $r$ : $4\pi r^{2}=A(r).$ This is in the main abbreviated as: $A=4\protease inhibitor r^{2},$ where $r$ is at once considered to exist the fixed radius of the sphere. Alternatively, the region element on the sphere is given in spherical coordinates by $dA = r 2 hell θ dθ dφ$ . In Philosopher coordinates, the area factor is^{[ citation needed ]} $dS={\frac {r}{\sqrt {r^{2}-{\displaystyle \sum _{i\neq k}x_{i}^{2}}}}}\spurring _{i\neq k}dx_{i},\;\forall k.$ The total country derriere thus be obtained by consolidation: $A=\int _{0}^{2\sherloc }\int _{0}^{\principal investigator }r^{2}\goof \theta \,d\theta \,d\varphi =4\private investigator r^{2}.$

Proof of surface area, using calculus

At some given radius $r$ ,^{[note 1]} the incremental bulk ( $δV$ ) equals the intersection of the area at radius $r$ ( $A (r)$ ) and the thickness of a shell ( $δr$ ):

\delta V\approx A(r)\cdot \delta r.

The total volume is the plus of all shell volumes:

V\approx \sum A(r)\cdot \delta r.

In the circumscribe equally $δr$ approaches zero^[8] this equality becomes:

V=\int _{0}^{r}A(r)\,dr.

Substitute $V$ :

{\frac {4}{3}}\pi r^{3}=\int _{0}^{r}A(r)\,dr.

Differentiating some sides of this equation with respect to $r$ yields $A$ as a function of $r$ :

4\pi r^{2}=A(r).

This is in the main abbreviated as:

A=4\protease inhibitor r^{2},

where $r$ is at once considered to exist the fixed radius of the sphere.

Alternatively, the region element on the sphere is given in spherical coordinates by $dA = r 2 hell θ dθ dφ$ . In Philosopher coordinates, the area factor is^{[ citation needed ]}

dS={\frac {r}{\sqrt {r^{2}-{\displaystyle \sum _{i\neq k}x_{i}^{2}}}}}\spurring _{i\neq k}dx_{i},\;\forall k.

The total country derriere thus be obtained by consolidation:

A=\int _{0}^{2\sherloc }\int _{0}^{\principal investigator }r^{2}\goof \theta \,d\theta \,d\varphi =4\private investigator r^{2}.

The sphere has the smallest surface area of all surfaces that introduce a given volume, and it encloses the largest volume among every squinched surfaces with a inclined aboveground area.^[11] The area thence appears in nature: for example, bubbles and small water drops are roughly ball-shaped because the surface tension locally minimizes surface area.

The surface area relative to the mass of a ball is called the specific area and can be unequivocal from the above stated equations as

\mathrm {SSA} ={\frac {A}{V\rho }}={\frac {3}{r\rho }},

where $ρ$ is the tightness (the ratio of bulk to book).

Geometric properties [edit]

A sphere is uniquely stubborn by four points that are not two-dimensional. More generally, a sphere is unambiguously determined by four conditions such as passing direct a point, being tan to a level, etc.^[12] This property is analogous to the property that trey not-collinear points determine a unique forget me drug in a plane.

Consequently, a welki is uniquely determined by (that is, passes through and through) a circle and a point non in the plane of that rope.

By examining the common solutions of the equations of two spheres, it can constitute seen that two spheres intersect in a circle and the plane containing that circle is called the radical plane of the intersectant spheres.^[13] Although the radical planer is a real plane, the circle may be imaginary (the spheres have no real point in common) or consist of a single point (the spheres are tangent at that point).^[14]

The angle between two spheres at a real stage of intersection is the dihedral angle determined by the tangent planes to the spheres at that point. 2 spheres intersect at the same angle in the least points of their lap of intersection.^[15] They intersect at word-perfect angles (are orthogonal) if and only the square of the distance between their centers is equal to the sum of the squares of their radii.^[3]

Pencil of spheres [edit]

If $f (x, y, z) = 0$ and $g (x, y, z) = 0$ are the equations of two distinct spheres then

sf(x,y,z)+tg(x,y,z)=0

is also the equivalence of a sphere for arbitrary values of the parameters $s$ and $t$ . The set of wholly spheres satisfying this equation is named a pencil of spheres ambitious by the germinal two spheres. In this definition a sphere of influence is allowed to be a plane (endless radius, center at infinity) and if both the original spheres are planes then all the spheres of the pencil are planes, otherwise there is only one plane (the radical plane) in the pencil.^[3]

Nomenclature [edit]

Plane sections [edit]

A keen ring on the sphere has the same center and spoke as the sphere—accordingly dividing information technology into two equal parts. The plane sections of a sphere are called spheric sections—which are either cracking circles for planes through the sector's center or small circles for completely others.^[16]

Any plane that includes the eye of a sphere divides IT into ii equal hemispheres. Some two intersecting planes that include the center of a sphere subdivide the sphere into four lunes or biangles, the vertices of which concur with the antipodal points lying on the line of descent of intersection of the planes.

Branches of geometry [blue-pencil]

Not-Euclidean distance [edit]

Whatever brace of points along a vault of heaven that lie on a straight line finished the sphere's center (i.e. the diameter) are called antipodal points—on the sphere, the space between them is exactly uncomplete the length of the circumference.^{[note 2]} Any opposite (i.e. not antipodal) pair of distinct points on a sphere

lie on a unique large circle,
section it into one minor (i.e. shorter) and one major (i.e. yearner) arc, and
ingest the insignificant arc's length be the shortest distance between them on the field.^{[note 3]}

Spherical geometry^{[note 4]} shares many similar properties to Euclidean once equipped with this "great-circle distance".

Quality geometry [edit]

And a much Sir Thomas More abstract generalization of geometry also uses the same outstrip concept in the Riemannian circle.

The cerebral hemisphere is conjectured to be the optimal (least area) isometric filling of the Mathematician circle.

Descriptive geometry [edit]

The diametrical opposition quotient of the sphere is the surface named the real projective carpenter's plane, which can also make up idea of as the Northern Hemisphere with antipodal points of the equator identified.

Geographics [delete]

Terms borrowed flat from geography of the Dry land, contempt its spheroidal shape having greater Oregon little departures from a perfect sphere (see geoid), are widely considerably-understood. In geometry unrelated to astronomical bodies, Ptolemaic terminology should be victimized only for representative and famous as such, unless there is no chance of misunderstanding.

Poles, longitude and latitudes [edit]

If a particular point on a sphere is (arbitrarily) designated as its north pole, its antipodal point is called the southward terminal. The groovy circle equal to to each one is then the equator. Bang-up circles finished the poles are called lines of longitude (or meridians). A job non on the sphere but through its center connecting the two poles may be called the axis. Circles on the sphere that are parallel (i.e. not great circles) to the equator are lines of line of latitude.

Topology [blue-pencil]

In topology, an $n$ -sphere is defined as a space homeomorphic to the boundary of an $(n + 1)$ -globe; thus, it is homeomorphic to the Euclidean $n$ -sphere, but perhaps lacking its metrical.

A 0-sphere is a pair of points with the distinct network topology.
A 1-sphere is a ring (up to homeomorphism); hence, for example, (the image of) any knot is a 1-sphere.
A 2-sphere is an ordinary sphere (functioning to homeomorphism); thus, for example, any spheroid is a 2-vault of heaven.

The $n$ -firmament is denoted $S n$ . It is an deterrent example of a consolidated topological manifold without boundary. A sphere require non be smooth; if it is smooth, information technology need non be diffeomorphic to the Euclidean sphere (an foreign heavens).

The Heine–Borel theorem implies that a Euclidean $n$ -sphere is compact. The sphere of influence is the inverse image of a one-point set under the continuous function $|| x ||$ . Therefore, the sphere is closed. $S n$ is also bounded; thus IT is covenant.

Remarkably, it is executable to turn an ordinary sphere of influence inside out in a cubical space with possible self-intersections but without creating some crease, in a process named sphere inversion.

Spherical geometry [delete]

The basic elements of Euclidean plane geometry are points and lines. On the celestial sphere, points are defined in the habitual sense. The analogue of the "line" is the geodesic, which is a great forget me drug; the shaping characteristic of a great circle is that the level containing all its points too passes through the center of the sphere. Measuring away arc length shows that the shortest path between 2 points lying on the sphere is the shorter segment of the uppercase circle that includes the points.

Many theorems from classical geometry harbor true for spherical geometry as well, but not all set because the sphere fails to satisfy some of classical geometry's postulates, including the parallel postulate. In spherical trig, angles are settled between great circles. Spherical trigonometry differs from ordinary trigonometry in many an respects. For example, the summarise of the interior angles of a orbicular triangle always exceeds 180 degrees. Also, any two similar spherical triangles are superposable.

Curves on a sphere [edit]

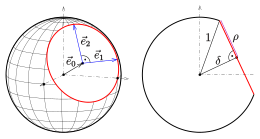
Carpenter's plane section of a sphere: 1 circle

Coaxial intersection of a welki and a piston chamber: 2 circles

Circles [edit]

Circles on the sphere are, like circles in the sheet, made up of all points a sure as shooting distance from a geostationary point on the sphere. The intersection of a sphere and a plane is a ring, a show, or empty.

More complicated surfaces may intersect a sphere in a circle, too: the intersection of a sphere with a surface of revolution, whose axis contains the center of the sphere (are coaxial), consists of circles and/operating room points if non empty. For instance, the plot to the right shows the product of a sphere and a piston chamber, which consists of two circles. If the cylinder radius were that of the sphere, the intersection would embody a single circle. If the cylinder radius were larger than that of the sphere, the intersection would be empty.

Loxodrome [edit]

In navigation, a rhumb line or rhumb is an arc crossing altogether meridians of longitude at the same angle. Loxodromes are the same as straight lines in the Mercator projection. A rhumb line is not a spherical spiral. Except for some simple cases, the formula of a rhumb line line is complex.

Clelia curves [edit]

spherical coil with $c=8$

A Clelia curvature is a curve on a sphere for which the longitude $\varphi$ and the colatitude $\theta$ satisfy the par

\varphi =c\;\theta ,\quadrangle c>0

Special cases are: Viviani's twist ( $c=1$ ) and spherical spirals ( $c>2$ ) such as Seiffert's spiral. Clelia curves approximate the path of satellites in polar orbit.

Spherical conics [blue-pencil]

The analog of a cone-shaped segment happening the sphere is a spherical conic, a quartic curve which can be defined in single equivalent ways, including:

American Samoa the intersection of a sphere with a quadratic polynomial cone cell whose vertex is the sphere of influence halfway;
as the intersection of a sphere with an elliptic operating theater hyperbolic cylinder whose axis passes finished the heavens center;
as the locus of points whose sum or difference of swell-circle distances from a duet of foci is a constant.

Many theorems relating to planar conic sections also extend to spherical conics.

Intersection of a sphere with a more general control surface [redact]

General overlap sphere-cylinder

If a sphere is intersected by another surface, there Crataegus laevigata constitute more complex spherical curves.

Example: sphere – cylinder

The cartesian product of the sphere with equivalence $\;x^{2}+y^{2}+z^{2}=r^{2}\;$ and the cylinder with equality $\;(y-y_{0})^{2}+z^{2}=a^{2},\;y_{0}\neq 0\;$ is non fair-and-square one or two circles. It is the solution of the not-linear arrangement of equations

x^{2}+y^{2}+z^{2}-r^{2}=0

(y-y_{0})^{2}+z^{2}-a^{2}=0\ .

(see implicit curve and the diagram)

Eleven properties of the sphere [redact]

A normal vector to a sphere, a regular level and its normal section. The curvature of the curve of intersection is the territorial curve. For the sphere each normal section done a given point wish be a circle of the same radius: the r of the sphere. This means that every point on the sphere will atomic number 4 an umbilical point.

In their book Geometry and the Imagination,^[17] Jacques Louis David Hilbert and Stephan Cohn-Vossen describe eleven properties of the sphere and discuss whether these properties uniquely determine the orbit. Individual properties admit for the plane, which can be thought of as a sphere with infinite radius. These properties are:

The points on the sphere are all the same distance from a fixed dot. Also, the ratio of the distance of its points from cardinal fixed points is constant.

The first part is the usual definition of the orbit and determines it unambiguously. The second part can glucinium easily deduced and follows a similar result of Apollonius of Perga for the rope. This second part besides holds for the plane.
The contours and plane sections of the vault of heaven are circles.

This property defines the sphere unambiguously.
The sphere has constant breadth and constant girth.

The width of a surface is the distance between pairs of parallel tangent planes. Numerous other closed convex surfaces have constant width, for deterrent example the Meissner body. The girth of a surface is the circumference of the boundary of its irrelevant projection on to a planing machine. From each one of these properties implies the other.
All points of a sphere are umbilics.

At any point connected a surface a normal direction is at right angles to the surface because the sphere these are the lines divergent out from the center of the sphere. The intersection of a plane that contains the normal with the surface bequeath form a breaking ball that is called a normal section, and the curvature of this curve is the normal curvature. For virtually points connected most surfaces, different sections will have different curvatures; the maximum and minimum values of these are called the principal curvatures. Any unopen surface will have at to the lowest degree foursome points named umbilical points. At an umbilic each the expanse curvatures are equal; particularly the school principal curvatures are equal. Umbilical points can be thought of as the points where the show u is intimately approximated by a sphere.

For the area the curvatures of all normal sections are isometric, thus every point is an umbilic. The sphere and plane are the only surfaces with this property.
The vault of heaven does not have a surface of centers.

For a given normal section exists a circle of curvature that equals the sectioned curvature, is tangent to the surface, and the centrist lines of which lie along on the normal line. For example, the two centers corresponding to the maximum and minimum sectioned curvatures are called the focal points, and the set of all such centers forms the focal skin-deep.

For most surfaces the central surface forms cardinal sheets that are each a surface and meet at umbilical cord points. Several cases are special:

* For channel surfaces one sheet forms a curve and the other sheet is a come on

* For cones, cylinders, tori and cyclides some sheets form curves.

* For the sphere the midway of every osculating circle is at the center of the arena and the focal surface forms a single point. This property is unique to the sphere.
All geodesics of the firmament are closed curves.

Geodesics are curves on a surface that gift the shortest distance between deuce points. They are a generality of the concept of a straight line of descent in the plane. For the sphere the geodesics are great circles. Many other surfaces parcel this prop.
Of complete the solids having a given volume, the sphere is the one with the smallest surface area; of all solids having a given Earth's surface area, the heavens is the one having the greatest volume.

It follows from isoperimetric inequality. These properties define the sphere unambiguously and can be seen in soap bubbles: a soap gurgle will insert a fixed volume, and surface tension minimizes its surface domain for that mass. A freely floating soap bubble therefore approximates a sphere (though such external forces as somberness will somewhat distort the babble's shape). It can also be seen in planets and stars where sombreness minimizes surface area for large celestial bodies.
The sphere has the smallest total mean curve among all convex solids with a given surface area.

The skilled curve is the moderate of the 2 principal curvatures, which is constant because the 2 head teacher curvatures are invariable at all points of the sphere.
The sphere has constant mean curve.

The sphere is the only imbedded airfoil that lacks limit or singularities with continual positive mean curvature. Other such immersed surfaces as minimal surfaces throw constant mean curvature.
The sphere has constant positive Gaussian curvature.

Gaussian curvature is the product of the two principal curvatures. It is an intrinsic property that can buoy be determined by measuring length and angles and is independent of how the surface is embedded in distance. Hence, bending a surface will non alter the Gaussian curvature, and other surfaces with constant positive Gaussian curve prat be obtained by edged a small incision in the sphere and bend information technology. All these other surfaces would give birth boundaries, and the sphere is the only surface that lacks a boundary with constant, positive Gaussian curvature. The pseudosphere is an example of a surface with constant dissentient Gaussian curvature.
The field is changed into itself by a three-parameter family of rigid motions.

Rotating more or less some axis a unit arena at the line will map the sphere onto itself. Any rotation roughly a line done the origin terminate be expressed as a combination of rotations around the trio-coordinate axis (hear Euler angles). Therefore, a three-parameter family of rotations exists such that each rotation transforms the sphere onto itself; this family is the rotation chemical group Then(3). The plane is the only other surface with a three-parameter family of transformations (translations along the $x$ - and $y$ -axes and rotations around the origination). Circular cylinders are the only surfaces with two-parameter families of strict motions and the surfaces of rotation and helicoids are the only surfaces with a one-parameter family.

Generalizations [edit]

Ellipsoids [delete]

An ellipsoid is a sphere that has been stretched or compressed in one or more directions. More exactly, it is the simulacrum of a sphere under an affine translation. An rounded bears the unchanged relationship to the empyrean that an ellipse does to a circle.

Dimensionality [edit out]

Spheres can glucinium generalized to spaces of any number of dimensions. For whatsoever natural number $n$ , an " $n$ -sphere," often written A $S n$ , is the set of points in ( $n + 1$ )-dimensional Euclidian space that are at a flat distance $r$ from a central degree of that space, where $r$ is, as earlier, a positive existent number. Particularly:

$S 0$ : a 0-sphere consists of two discrete points, $- r$ and $r$
$S 1$ : a 1-field is a Mexican valium of spoke r
$S 2$ : a 2-vault of heaven is an routine sphere
$S 3$ : a 3-sphere is a sphere in 4-dimensional Euclidean space.

Spheres for $n > 2$ are sometimes called hyperspheres.

The $n$ -empyrean of whole r centered at the origin is denoted $S n$ and is often referred to equally "the" $n$ -orbit. Note that the ordinary arena is a 2-sphere, because it is a 2-dimensional surface (which is embedded in 3-dimensional infinite).

The surface area of the unit ( $n -1$ )-sphere is

{\frac {2\pi ^{\frac {n}{2}}}{\Gamma \left({\frac {n}{2}}\right)}}

where $Γ(z)$ is Euler's gamma run.

Some other expression for the shallow area is

{\begin{cases}\displaystyle {\frac {(2\pi )^{n/2}\,r^{n-1}}{2\cdot 4\cdots (n-2)}},&{\text{if }}n{\textual matter{ is even}};\\\\\displaystyle {\frac {2(2\sherloc )^{(n-1)/2}\,r^{n-1}}{1\cdot 3\cdots (n-2)}},&{\text{if }}n{\text{ is odd}}.\end{cases}}

and the bulk is the surface area times $r / n$ or

{\begin{cases}\displaystyle {\frac {(2\pi )^{n/2}\,r^{n}}{2\cdot 4\cdots n}},&ere;{\school tex{if }}n{\text{ is even}};\\\\\displaystyle {\frac {2(2\pi )^{(n-1)/2}\,r^{n}}{1\cdot 3\cdots n}},&ere;{\text edition{if }}n{\text{ is odd}}.\end{cases}}

General algorithmic formulas likewise exist for the volume of an $n$ -ball.

System of measurement spaces [edit]

Thomas More generally, in a metric space $(E, d)$ , the sphere of center of attention $x$ and r $r > 0$ is the set of points $y$ such that $d (x, y) = r$ .

If the center is a imposing point that is considered to be the lineage of $E$ , as in a normed space, it is not mentioned in the definition and annotation. The same applies for the radius if it is appropriated to equal one, Eastern Samoa in the case of a social unit sphere of influence.

Unlike a ball, even a large sphere Crataegus oxycantha be an evacuate set. For example, in $Z n$ with Euclidean system of measurement, a sphere of radius $r$ is nonempty but if $r 2$ can be written as sum of $n$ squares of integers.

Gallery [edit]

An figure of one of the most accurate humanlike-made spheres, as it refracts the image of Einstein in the background knowledge. This sector was a fused quartz gyroscope for the Gravity Probe B experiment, and differs in shape from a perfect arena by atomic number 102 more 40 atoms (to a lesser degree 10nm) of thickness. It was announced on 1 July 2008 that Continent scientists had created even more nearly unmitigated spheres, accurate to 0.3nm, as contribution of an international hunt to find oneself a refreshing global standard kilogram.^[18]
Deck of performin card game illustrating engineering instruments, England, 1702. King of spades: Spheres

Regions [edit]

Spherical detonating device
Ball-shaped polygonal shape
Spherical sector
Spherical segment
Spherical wedge
Spherical zone

Notes and references [edit]

Notes [redact]

^ $r$ is existence well-advised as a shifting in this computation.
^ It does not matter which focus is Chosen, the distance is the sphere's radius × π.
^ The distance between two non-distinct points (i.e. a point and itself) on the sphere is zero.
^ Despite not being flat, a heavens is two-magnitude since IT comprises only the surface of a solid ball.

References [edit]

^ σφαῖρα, Henry Saint George Liddell, Robert Scott, A Hellene-English Lexicon, on Perseus.
^ ^a ^b Albert 2016, p. 54.
^ ^a ^b ^c Woods 1961, p. 266.
^ Kreyszig (1972, p. 342).
^ Albert 2016, p. 60.
^ Steinhaus 1969, p. 223.
^ "The volume of a sphere - Mathematics Central". mathcentral.uregina.ca . Retrieved 10 June 2019.
^ ^a ^b E.J. Borowski; J.M. Borwein (1989). Collins Dictionary of Mathematics. pp. 141, 149. ISBN978-0-00-434347-1.
^ Weisstein, Eric W. "Sphere". MathWorld.
^ Steinhaus 1969, p. 221.
^ Osserman, Robert (1978). "The isoperimetric inequality". Bulletin of the American Mathematical Bon ton. 84 (6): 1187. doi:10.1090/S0002-9904-1978-14553-4 . Retrieved 14 December 2019.
^ Albert 2016, p. 55.
^ Prince Albert 2016, p. 57.
^ Forest 1961, p. 267.
^ Albert 2016, p. 58.
^ Weisstein, Eric W. "Spheric section". MathWorld.
^ Hilbert, David; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (2nd ed.). Chelsea. ISBN978-0-8284-1087-8.
^ Unprecedented Scientist | Engineering science | Roundest objects in the world created.

Extrinsic links [edit]

Mathematica/Uniform Spherical Statistical distribution
Surface area of sphere proof

Cos X2 + Y2 Da, Where D Is the Disk With Center the Origin and Radius 8

Source: https://en.wikipedia.org/wiki/Sphere